【深める】格差に関する指標について②「ジニ係数」
ジニ係数の概要
格差を端的に数値で示すものだ。
ローレンツ曲線では時系列比較や国際比較がしにくい。
ジニ係数だとそれが可能。
所得分配の不平等(所得格差)がない状態を0とし、不平等が拡大すれば1の値に近づく係数である。
「数値が0に近いほど格差が少ない」と覚えておくとよい。
一般的な目安は「0.5」と言われており、この数値を超えると所得格差がかなり大きい状態とされる。
日本は2005年に0.5を超え、現在も高止まりしている。
累進課税制度・社会保障制度等による「再分配所得ジニ係数」も0.37前後で推移、アメリカ、イギリスより低いが、フランス、ドイツより高く、格差は主要国の中では高い。

ジニ係数の計算式
「45度線とローレンツ曲線にはさまれた部分の面積」と「45度線の下の三角形の面積」の比で表す。
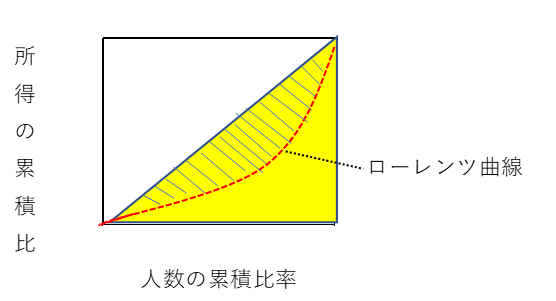
その計算式は、「三日月の面積」÷「45度線の三角形の面積」
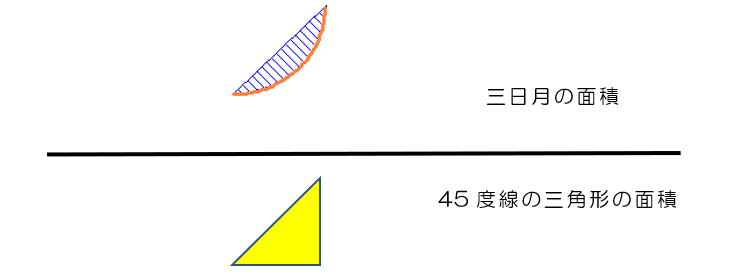
三日月の面積が大きいほどジニ係数も増大、格差が拡大していることになる。
ローレンツ曲線のところで見た曲線Aと曲線B、45度線から離れ右下に膨らんだ曲線Bのほうが格差社会であったことを想起すれば、この点も理解できるはず。
で、共通テストでは、どのように出題される可能性があるのか。
例題1 正誤問題(ジニ係数の基本)
まずは簡単な正誤問題。一つだけ誤りがある。どれか。
誤りは②。
所得分布全体に占める低所得層の比率は「相対的貧困率」。
後に詳しく見るが、これを知らないと案外否定文ということで③あたりを選ぶ受験生もいるかも。
④は正しいと判断できないといけない。
「ジニ係数が1に近いほど格差が大きい」という文章が出たら、これも○。
例題2 正誤問題(ジニ係数とローレンツ曲線)
次に、ジニ係数はローレンツ曲線をもとに作成されるので、両者が混在した問題も出題される可能性がある。以下のうち一つだけ正しいものがある。どれか。
①ローレンツ曲線は、所得が高い世帯から並べた場合の累積比率を現す。
②45度線から離れたローレンツ曲線ほど格差が少ない状況であることを意味する。
③ジニ係数は、45度線の下の三角形と、45度線とローレンツ曲線とで囲まれる部分との面積の比である。
④ジニ係数が1に近いほど格差は小さい。
正解は③。
これはローレンツ曲線のグラフを視覚的に理解していれば○と判断できるが、その学習をしていなかったらちんぷんかんぷんかも。
ただし、ローレンツ曲線・ジニ係数の基礎的な知識があれば①②④が誤りと判断でき、消去法で③を選ぶこともできる。
①は「所得が低い世帯」から並べたもの、②逆で、離れた曲線ほど格差が大きい。
④逆で、1に近いほど格差は大きい。
例題3 ローレンツ曲線の計算(共通テスト予想問題)
最後に、場合によっては、計算問題の出題もない訳ではない。
これまでセンター試験・共通テストでは出題実績はないが、出題されたら大きな差が出るはず。
この場合、共通テストレヴェルでは、「ジニ係数は、45度線とローレンツ曲線にはさまれた部分の面積と45度線の下の三角形の面積の比で表す。」といった定義=ヒントを示したうえで、以下のような問い方が想定される。
まず表とグラフの理解から確認しておこう。
①表から読み取れること
・総世帯数が300、
・累積所得が(100万✕100)+(300万✕100)+(400万✕100)
=800万✕100
=8億円であることを押さえたい。
②グラフから読み取れること

・グラフの1/3地点(オレンジ)は、
世帯数の1/3 (300人中の100人)が累積所得(100万✕100=1億円)で、
全体の1/8を所有していることを示している。
・2/3地点(オレンジ+グリーン)では、
さらにグリーン部分、300万の平均所得である1/3の世帯(300人中の100人)が加わって、
累積所得は1億+3億=4億円で、
全体の4/8、つまりは半分を占めることになる。
・全体(オレンジ+グリーン+ブルー)
最後にここに400万の平均所得である1/3の世帯(300人中の100人)が加わり完結する。
累積所得は1億+3億+4億=8億(表から読み取れることと一致)
グラフは上記のような累積を示したものである。
③ジニ係数の計算
このグラフをもとにジニ係数を計算することになる。
ジニ係数の計算式は、「三日月の面積」÷「45度線の三角形の面積」
・まず、「45度線の三角形の面積」は、1 × 1 × 1/2 = 1/2
・「三日月の面積」
考え方としては、計算公式の45度線からの「三日月」に囚われていてはダメ。
逆に「三日月」でないところ、ローレンツ曲線の右側の面積を出してやり、三角形の面積からそれを引いてやると「三日月」の面積を求めてやることができる。
「三日月の面積」=「45度線の三角形の面積」 ー (オレンジ+グリーン+ブルー)

丁寧に見ていくと
・オレンジ部分の面積が・・・
1/3 × 1/8 × 1/2 = 1/48
・グリーン部分の面積が・・・台形の面積の公式から
(1/8 + 4/8) × 1/3 × 1/2 = 5/48
・ブルー部分の面積が・・・同じく台形の面積の公式から
(4/8 + 1 ) × 1/3 × 1/2 = 12/48
「三角形」の面積は1/2なので
したがって、「三日月の面積」は、
1/2 - (1/48 + 5/48 + 12/48) = 1/8
・よって、ジニ係数は、
1/8 ÷ 1/2 = 1/4 = 0.25
※ジニ係数は「三日月」の面積✕2という計算式でももとめることができる。
1/8 × 2 = 1/4 = 0.25
さすがにこんな時間のかかる問題は出ないかも知れないが、理解できたであろうか?
こうした確認をしておくと、ジニ係数についての理解もきっと深まったはずだ。
急がば回れである。
